MATEMATICA

Números y Funciones

Función

En matematicas, se dice que una magnitu o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadro del radio, A = π·r². Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, T = d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.

En álgebra abstracta, el concepto general de función, aplicación o mapeo se refiere en a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto. Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):

...	−2 → +4,	−1 → +1,	±0 → ±0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:

...,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Avión → A,

...

 

 

Función monótona 

 

Sea

 

 

Una función entre dos conjuntos P y Q, donde cada conjunto tiene un orden parcial (los dos se denotarán por ≤). En cálculo se habla de funciones entre subconjuntos de los reales, y el orden ≤ no es otro que el orden usual de la recta real, aunque esto no es esencial para la definición.

La función f es monótona si y solo si x ≤ y implica f(x) ≤ f(y) (es decir, la función es creciente), o bien x ≤ y implica f(x) ≥ f(y) (es decir, la función es decreciente). En otras palabras, una función es monótona si conserva el orden.

Monotonía  en cálculos y análisis 

En cálculo no hay usualmente necesidad de invocar los métodos abstractos de la teoría del orden. Como ya se señaló, las funciones se establecen entre (subconjuntos de) números reales, ordenados de forma natural.

Por la forma de la grafica de una función monótona en los reales, tales funciones se llaman también monótonamente crecientes (o no decreciente), respectivamente.

Ejemplo gráfico

A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente por la izquierda y por la derecha, mientras que es constante en el medio; por lo demás, es creciente pues conserva el orden ascendente durante todo el recorrido de la función. La segunda de ellas es escrictamente decreciente por la izquierda y por la derecha, puesto que conserva el orden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta maximo y minimos relatívos).

 

 

Variación monotonía

Crecimiento puntual

Una función f(x) es creciente en x=a si existe δ>0 / para todo x perteneciente a (a - δ,a)f(x) < f(a) y para todo x perteneciente a (a,a + δ)f(x) > f(a).

f es creciente en x=a.

Análogamente se define el decrecimiento puntual.

Condición suficiente para el crecimiento puntual

Si en un punto a la función f(x) tiene derivada positiva, la función es creciente en a.

H) f'(a)>0
T) f es creciente en x=a.

Demostración:

            f(x) - f(a)

f'(a) = lim ----------- > 0 => (por teo. de conservación del signo)

        x->a   x - a

                                                 f(x) - f(a)

existe δ>0 / para todo x perteneciente al E*a,δ  ----------- > 0

                                                    x - a

 

1) Si x < a => x - a < 0 => f(x) - f(a) < 0 => f(x) < f(a)

2) Si x > a => x - a > 0 => f(x) - f(a) > 0 => f(x) > f(a)

 

De 1) y 2) por def. de crecimiento puntual,

f es creciente en x=a.

Teorema

Condición suficiente para el decrecimiento puntual

Si en un punto a la función f(x) tiene derivada negativa, la función es decreciente en a.

H) f'(a)<0
T) f es decreciente en x=a.

La demostración es análoga a la anterior.

Definición

Máximo relativo

f(x) presenta un máximo relativo en x=a si existe un E*a / para todo x perteneciente al E*a f(x) < f(a).

f presenta un máximo relativo en x=a.

Definición

Mínimo relativo

f(x) presenta un mínimo relativo en x=a si existe un E*a / para todo x perteneciente al E*a f(x) > f(a).

f presenta un mínimo relativo en x=a.

Teorema

Condición necesaria para la existencia de extremos relativos

Si una función f(x) es derivable en un punto a, es condición necesaria para que presente un extremo relativo en a que f'(a) valga 0.

H) f presenta un extremo relativo en x=a
    Existe f'(a)
T) f'(a)=0

Demostración:

Si f'(a) > 0 => por Cond. suf. para el crecimiento puntual f es creciente en x=a. Absurdo.

Si f'(a) < 0 => por Cond. suf. para el decrecimiento puntual f es decreciente en x=a. Absurdo.

=> f'(a) = 0.

Nota: El recíproco no es cierto. Una función puede tener derivada nula en un punto y no tener un extremo relativo en el punto.

Contraejemplo: f(x) = x3

f'(0) = 0 pero f no presenta un extremo en 0.

 

Definición

Función monótona creciente en un intervalo.

f es monótona creciente en (a,b) si para todo x1 y para todo x2pertenecientes a (a,b), tales que x1 < x2, se cumple que f(x1) < f(x2).

f es monótona creciente en [a,b] si es monótona creciente en (a,b) y para todo x perteneciente a (a,b) se cumple que f(a) < f(x) < f(b).

Análogamente se define función monótona decreciente.

Teorema

Condición suficiente para el crecimiento en un intervalo abierto

Si en un intervalo abierto (a,b) la función f(x) tiene derivada positiva, f(x) es creciente en (a,b).

H) f'(x)>0 para todo x perteneciente a (a,b)
T) f es creciente en (a,b)

Demostración:

Sean x1, x2 pertenecientes a (a,b), x1 < x2.
f es derivable en [x1,x2] => por teo. de Lagrange existe c perteneciente a [x1,x2] /

        f(x2) - f(x1) 

f'(c) = ------------- > 0

           x2 - x1

x2 - x1 > 0 => f(x2) - f(x1) > 0 => f(x2) > f(x1) => por def. de función creciente en un intervalo f es creciente en (a,b).

Ejemplo

f:R+ -> R / f(x) = Lx f'(x) = 1/x > 0 para todo x > 0 => f es creciente para todo x > 0.

Teorema

Condición suficiente para el decrecimiento en un intervalo abierto

H) f'(x)<0 para todo x perteneciente a (a,b)
T) f es decreciente en (a,b)

Demostración análoga a la anterior

Teorema

Condición suficiente para la existencia de mínimo relativo

Si una función es continua en un punto a, y existe un entorno de a tal que la derivada de f es negativa en el semientorno izquierdo y positiva en el semientorno derecho, entonces f presenta un mínimo relativo en a.

H) f es continua en x=a.
Existe δ>0 / para todo x perteneciente a (a-δ,a) f'(x)<0 y para todo x perteneciente a (a,a+δ) f'(x)>0 
T) f presenta un mínimo relativo en x=a.

Demostración

Sea x1 perteneciente a (a-δ,a).
f es derivable en [x1,a] por hipótesis.
=> por teo. de Lagrange existe c1 perteneciente a (x1,a) /

          f(x1) - f(a)      

f'(c1) = ------------ < 0

            x1 - a   

x1 - a < 0 => f(x1) > f(a) (1)

Sea x2 perteneciente a (a,a+δ).
f es derivable en [a,x2] por hipótesis.
=> por teo. de Lagrange existe c2 perteneciente a (a,x2) /

         f(x2) - f(a)      

f'(c2) = ------------ > 0

            x2 - a   

x2 - a > 0 => f(x2) > f(a) (2)

De 1) y 2): para todo x perteneciente al E*a,δ f(x) > f(a) => por definición, f presenta un mínimo relativo en x=a

Ejemplo

f(x)=x2 f'(x)=2x            -   0   + sg 2x ---------|--------->                0

f presenta un mínimo relativo en x=0. (En este caso, es también el mínimo absoluto de la función.)

Condición suficiente para la existencia de máximo relativo

H) f es continua en x=a.
Existe δ>0 / para todo x perteneciente a (a-δ,a) f'(x)>0 y para todo x perteneciente a (a,a+δ) f'(x)<0 
T) f presenta un máximo relativo en x=a.

La demostración es análoga a la anterior.

Ejemplo

f(x)=-x2 f'(x)=-2x             +   0   - sg -2x ---------|--------->                 0

f presenta un máximo relativo en x=0. (En este caso, es también el máximo absoluto de la función.)

Monotonía de una función

La monotonía consiste en estudiar como aumenta o disminuye la variable dependiente   y   al aumentar o disminuir la variable independiente   x .

                     
 

Crecimiento de una función

Crecimiento de una función en un intervalo

Una función   f(x)   es estrictamente creciente en un intervalo   (a, b)   si para dos valores cualesquiera del intervalo   x1   y   x2   tales que   x1 < x2 , se cumple que   f(x1) < f(x2).

Decir que   f(x1) < f(x2)   es lo mismo que :

                        

Será creciente si   f(x1) ≤ f(x2)  , es decir:

                        

 

Una función es creciente si al aumentar la  'x' aumenta la 'y' .

 

Ejemplos de funciones estrictamente crecientes:

1)    f(x) = 2x

 

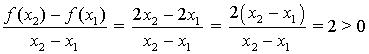
La función   f(x) = 2x   es estrictamente creciente en   R , ya que para dos puntos cualesquiera   x1   y   x2   obtenemos que:

 

               

 

2)    f(x) = x3

 

Es estrictamente creciente en   R , ya que para dos puntos cualesquiera   x1   y   x2   obtenemos que:

 

               

 

Observa la diferencia de los cubos.

Decrecimiento de una función

Decrecimiento de una función en un intervalo

Una función   f(x)   es estrictamente decreciente en un intervalo   (a, b)   si para dos valores cualesquiera del intervalo   x1   y   x2   tales que   x1 < x2 , se cumple que   f(x1) > f(x2) .

Decir que   f(x1) > f(x2)   es lo mismo que :

                        

Será creciente si   f(x1) ≥ f(x2)  , es decir:

                        

 

Una función es decreciente si al aumentar la  'x' disminuye la 'y' .

 

Ejemplo de función estrictamente creciente:

f(x) = 1/x

 

Es estrictamente decreciente en   [0 , ∞) , ya que para dos puntos cualesquiera   x₁   y   x₂   en dicho intervalo obtenemos que:

               

Ya que el denominador es siempre positivo.

                                            
 

Es estrictamente decreciente en   [-∞ , 0] . La demostración es la misma que en el caso anterior.

 

Decrecimiento de una función en un punto

Una función   f(x)   es estrictamente decreciente en un punto de abscisa   x₀   si existe un entorno simétrico de   x₀   en el que la función es estrictamente decreciente. Es decir:

 

               

 

Una función   f(x)   es decreciente en un punto de abscisa   x₀   si existe un entorno simétrico de   x₀   en el que la función es decreciente. Es decir:

 

               

Ejemplo de crecimiento y decrecimiento de una función

Determinar los intervalos de crecimiento y decrecimiento de la función:

 

            f(x) = x³ - 3x + 2

 

•   (-∞ , - 1):   la función es estrictamente creciente.

 

     Es decir, al aumentar la x, aumenta la y .

 

•   (- 1 , 1):   la función es estrictamente decreciente.

 

     Es decir, al aumentar la x, disminuye la y .

 

•   (1 , ∞):   la función es estrictamente creciente.

 

    Es decir, al aumentar la x, aumenta la y .

 

Simetría respecto del eje de ordenadas

Una función f es simétrica respecto del eje de ordenadas si ésta es una función par, es decir:

f(-x) = f(x)

Simetría respecto al origen

Una función f es simétrica respecto al origen si ésta es una función impar, es decir:

f(-x) = -f(x)

               

 Paridad de las funciones.

En matemáticas, se puede clasificar a las funciones según su paridad: Las funciones pueden ser pares, impares o no tener paridad.

Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares de simetría, con respecto a sus funciones inversas aditivas (funciones inversas aditivas u opuestas son funciones que al sumarlas el resultado es cero).

Función par: f(-x) =f(x)

Función impar:f(-x)=-f(x)

Las funciones pares e impares deben su nombre a la paridad de las potencias en las funciones de potencias que satisfacen cada condición: La función f(x)=xn: es una función par si n es un entero par, y es una función impar si n es un entero impar.

Ejemplos de funciones de x pares e impares:

                                          

Función lineal

En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b= 0 de la forma:

mientras que llaman función afín a la que tiene la forma:

cuando b es distinto de cero.

Ejemplo

Una función lineal de una única variable dependiente x es de la forma:

  Y=M X +B

que se conoce como ecuación de la recta en el plano x,y.

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

Y=0.5 X +2

en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.

En la ecuación:

la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.

En una recta el valor de m se corresponde al ángulo de inclinación de la recta con el eje de las x a través de la expresión:

La función lineal es del tipo:

y = mx

Su gráfica es una línea recta que pasa por el origen de coordenadas.

y = 2x

x	0	1	2	3	4
y = 2x	0	2	4	6	8

Ecuación de la recta

 

Una recta r es el conjunto de los puntos del plano, alineados con un punto P y con una dirección dada .

Ecuación vectorial de la recta

Si el punto P(x₁, y₁) es un punto de la recta r, el vector PX tiene igual dirección que v, luego es igual a v multiplicado por un escalar:

 

 

 

Pendiente

m es la pendiente de la recta.

La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.

Función identidad

f(x) = x

Su gráfica es la bisectriz del primer y tercer cuadrante.

 

Ceros de la función

Toda función cuadrática posee un máximo o un mínimo, que es el vértice de la parábola. Si la parábola tiene concavidad hacia arriba, el vértice corresponde a un mínimo de la función; mientras que si la parábola tiene concavidad hacia abajo, el vértice será un máximo.

Dada la función en su forma desarrollada: , la coordenada x del vértice será simplemente: . La coordenada y del vértice corresponde a la función f evaluada en ese punto.

Dada la forma canónica: , las coordenadas explícitas del vértice son: (h,k).

⇔== Determinar la ecuación conocidos tres puntos ==

Partiendo de la forma de la ecuación:

y conocidos tres puntos del plano xy por los que pasa una función polinómica de segundo grado:

se cumplira que:

con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.

Representando el sistema ordenado de forma convencional:

Con lo que podemos calcular los valores de los coeficientes:

También llamadas raíces, representa los valores de x cuya imagen tiene valor cero,(x;0). Al ser cuadrática se obtiene, como máximo, 2 valores, denominados xCeros de la función cuadrática

1

y x

2

.Para calcular los ceros de la función a partir de la ecuación polinómica aplicamo

 

                                                                                                                              

 

Sistema de dos ecuaciones

Explicación:

Hay varios métodos para resolver este tipo de sistemas:

MÉTODO DE SUSTITUCIÓN:

Primero se despeja una incógnita en una ecuación, y después se sustituye el resultado en la otra ecuación. Se puede despejar cualquier incógnita (o la x o la y) en cualquier ecuación (la primera o la segunda), pero siempre hay que sustituir en “la otra”, es decir, si despejamos en la primera ecuación, sustituimos en la segunda, y si despejamos en la segunda, sustituimos en la primera.

Por ejemplo, en el sistema:

3x + y = 5
4x-2y = 1

Despejamos la “y” en la primera ecuación:

y = 5 -3x

y sustituimos el resultado en “la otra” ecuación, es decir, en la segunda:

4x – 2(5 – 3x) = 1

obteniendo una ecuación con una incógnita, que ya podemos resolver.

MÉTODO DE IGUALACIÓN:

Primero se despeja la misma incógnita en las dos ecuaciones (o las dos x o las dos y) y después se igualan los resultados, obteniendo una sola ecuación con una sola incógnita. En el ejemplo anterior, si despejamos las dos y:

y = 5 – 3x
y = (4x – 1)/2

Igualando los resultados, obtenemos la ecuación con una incógnita:

5 – 3x = (4x – 1)/2

que ya podemos resolver.

MÉTODO DE REDUCCIÓN:

Primero tenemos que conseguir que una incógnita tenga el mismo coeficiente en las dos ecuaciones, pero cambiado de signo. Una vez conseguido, se suman las dos ecuaciones y así obtenemos una ecuación con una incógnita.

En el ejemplo anterior, si multiplicamos la primera ecuación por 2, conseguimos tener el mismo coeficiente (cambiado de signo) en las “y”:

2·(3x + y = 5) ---------------->6x + 2y = 10
4x – 2y = 1 ------------------->4x – 2y = 1

Sumando las dos ecuaciones entre sí:

10x = 11

donde ya podemos despejar la x.

REGLA DE CRAMER:

La Regla de Cramer (aplicable para sistemas de n ecuaciones con n incógnitas, haciendo uso de determinantes), puede simplificarse para el caso de n=2:

a x + b y = c
d x + e y = f

dando como resultado:

     x = (c·e – b·f ) / (a·e – b·d)
     y = (a·f – c·d) / (a·e – b·d)

Esto se conoce como la Regla de Cramer.

 

Inecuaciones

Representamos la región solución de la primera inecuación.

Transformamos la desigualdad en igualdad.

2x + y = 3

Damos a una de las dos variables dos valores, con lo que obtenemos dos puntos.

x = 0;     2 · 0 + y = 3;   y = 3;          (0, 3)

x = 1;     2 · 1 + y = 3;   y = 1;          (1, 1)

Al representar y unir estos puntos obtenemos una recta.

Tomamos un punto, por ejemplo el (0, 0), los sustituimos en la desigualdad. Si se cumple, la solución es el semiplano donde se encuentra el punto, si no la solución será el otro semiplano.

2x + y ≤ 3

2 · 0 + 0 ≤ 3       0 ≤ 3      Sí

 

Función de valor absoluto

Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:

1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.

2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.

3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.

4 Representamos la función resultante.

D=r

 

 

Intersecciones linales

La intersección de una recta son los puntos donde la recta intersecta, o cruza, los ejes horizontal y vertical.

 

La recta mostrada en la gráfica intersecta a los dos ejes de coordenadas. El punto donde la recta cruza el eje x se llama [intersección en x]. El punto [intersección en y] es donde la recta cruza el eje y.

 

 

 

Observa que la intersección en y ocurre cuando x = 0, y la intersección en x ocurre cuando y = 0.

 

Calculando Intersecciones

 

Podemos usar las características de las intersecciones para calcularlas rápidamente a partir de la ecuación de una recta. Puedes notar que es fácil, cuando encontramos las x- y y-intersecciones para la recta  .

 

Para encontrar la intersección en y, sustituimos 0 por x en la ecuación, porque sabemos que cada punto en el eje y tiene un valor de 0 en la coordenada x. Una vez hecha la sustitución, podemos resolver la ecuación para encontrar el valor de y. Cuando hacemos x = 0, la ecuación se convierte en , de donde se obtiene y = 2.  Por lo que, cuando x = 0, y = 2. Las coordenadas de la intersección en y son (0, 2).

 

Ejemplo
Problema	3y + 2x	=	6
	3y + 2(0)	=	6
	3y	=	6
Solución	y	=	2

 

Seguiremos ahora los mismos pasos para encontrar la intersección en x. Sea y = 0 en la ecuación, y resolvamos para x. Cuando y = 0, la ecuación se convierte en 3+2x=6, de donde se obtiene x = 3. Cuando y = 0, x = 3. Las coordenadas de la intersección en x son (3, 0).

 

Ejemplo
Problema	3y + 2x	=	6
	3(0) + 2x	=	6
	2x	=	6
		=
Solución	x	=	3

Hallar los puntos de intersección de la recta x + 2y + 1 = 0 y la circunferencia

x² + y² + 2x - 4y - 4 = 0

 

Resolución:

Funciones logarítmicas

 

 

Función logarítmica con la base mayor que 1

 

Función logarítmica con la base comprendida entre 0 y 1

 

            

 

Actividades interactivas

 

>   Comprueba la gráfica de la función logarítmica en función de su base.

 

Funciones trigonométricas

 

Función seno

    

 

Función coseno

    

 

Función tangente

Ceros de una función

 

Dada una función f: A ® B / y = f(x), se dice que x0 es un cero o raiz de f si y sólo si x0 Î A = Df y f(x0) = 0.

Los ceros de una función son los puntos en los que la gráfica corta al eje x. Así, en la siguiente gráfica, podemos ver que la función tiene tres ceros o raíces:

Entonces, encontrar los ceros o raíces de una función f: A ® B / y = f(x), implica resolver la ecuación f(x) = 0. Así, por ejemplo:

• la función y = x² + 1 no tiene ceros,
• la función y = x³ tiene un cero en x₀ = 0, y
• la función y = sen(x) tiene infinitos ceros en los valores de la forma x_k = k.p, con k entero.

3. FUNCION CUADRATICA

VARIACION

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:f (x) = a x ² + b x + c         ; su gráfico es una curva llamada parábola.

 

Autor: Leoncio Santos Cuervo

si la ecuación tiene todos los términos se dice ecuación completa, si a la función le falta el término lineal o independiente se dice que la ecuación es incompleta.

Dicha parábola tendrá algunas características o elementos bien definidos dependiendo de los valores de la ecuación que la generan.

Estas características o elementos son:

Orientación o concavidad (ramas o brazos)

Puntos de corte con el eje de abscisas (raíces)

Punto de corte con el eje de ordenadas

Eje de simetría

Vértice

Orientación o concavidad (ramas o brazos)

Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax²):

 

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x² − 3x − 5

 

 

Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x² + 2x + 3

 

Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.

Eje de simetría o simetría

Otra característica o elemento de la parábola es su eje de simetría.

El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; pasará por el punto medio entre estos, o sea se puede imaginar como un espejo que refleja la mitad de la parábola.

Su ecuación está dada por:

Donde  x₁  y  x₂  son las raíces de la ecuación de segundo grado en x, asociada a la parábola.

De aquí podemos establecer la ecuación del eje de simetría de la parábola:

 

Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)

Para calcular las raíces de cualquier función cuadrática calculamos f (x) = 0, es decir, los valores de x tales que y = 0. Como la ecuación ax² + bx +c = 0 posee un término de segundo grado, otro de primer grado y un término constante, no podemos aplicar las propiedades de las ecuaciones, entonces, para resolverla usamos la fórmula:

al resultado de la cuenta  b²  - 4ac se lo llama discriminante de la ecuación,

Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas).

Respecto a esta intersección, se pueden dar tres casos:

Que corte al eje X en dos puntos distintos

Que corte al eje X en un solo punto (es tangente al eje x)

Que no corte al eje X

Punto de corte en el eje de las ordenadas (eje de las Y)

En el eje de ordenadas (Y) la primera coordenada es cero, por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c). La abscisa de este punto corresponde al valor del eje de simetría y la ordenada corresponde al valor máximo o mínimo de la función,  según sea la orientación de la parábola (recuerde el discriminante)

https://www.profesorenlinea.cl/matematica/funcion_cuadratica.html                

Vértice

El vértice de la parábola está ubicado sobre la recta de simetría, de modo que su coordenada x, que será x_v vale:

En el vértice se calcula el máximo o (el mínimo) valor de la función de acuerdo a que la parábola tenga sus ramas hacia abajo o arriba; si la parábola no tiene raíces el vértice se puede calcular utilizando los coeficientes de la función de la siguiente manera:

https://www.dav.sceu.frba.utn.edu.ar/homovidens/Marcela%20Martinez/funcion_cuadratica_caracteristicas_nuevo.htm

 Máximos y Mínimos (función cuadrática)

La teoría de optimización clásica se usa para la obtención de los
máximos y mínimos de funciones no lineales restringidas y no restringidas, en los que 
se hace uso del cálculo diferencial.
Mínimo (fuerte): Un punto extremo X0 de una función f(X0) define un mínimo de la 
función si f(X0+h) > f(X0), donde X0  es cualquier punto de la función y h en valor 
absoluto es suficientemente pequeña.
Máximo (fuerte): Un punto extremo X0 de una función f(X0) define un máximo de la 
función si f(X0+h) < f(X0), donde X0  es cualquier punto de la función y h en valor 
absoluto es suficientemente pequeña.

 

 

 

https://vaneblog12.blogspot.com/2013/01/maximos-y-minimosfuncion-cuadratica.html

Cálculo de los máximos y mínimos relativos

f(x) = x³ − 3x + 2

Ejercicios

https://www.dervor.com/derivadas/maximos_mimimos.html

Ecuación cuadrática

Una ecuación cuadrática es una aquella en que el exponente mayor de la incógnita es 2. Es decir, es una ecuación de segundo grado, y al resolverla obtendrás dos soluciones posibles: x₁  y x₂ .       
La ecuación general de la ecuación de 2º grado o cuadrática es de la forma:

Ax²+ B x + C =0 (con A ? 0)

Para resolver una ecuación cuadrática existen diferentes métodos, dependiendo de los coeficientes numéricos A, B, C.

1.2 Resolución de ecuaciones cuadráticas

1. Por factorización 
Podremos resolver una  ecuación del tipo:   x²  - 12x -  28 = 0, por este método solo si el  trinomio puede ser factorizado. En este caso, buscando dos números que multiplicados den –28 y sumados den –12; (se buscan todos los pares de factores cuyo producto sea  28). En este ejercicio, los números son  -14 y 2, porque la suma de ellos es igual a  -12. Por lo tanto, la factorización es (x - 14)(x + 2) = 0. Como el producto es igual a 0, entonces (x – 14) = 0  o bien (x + 2) = 0.

Este método se puede aplicar en cualquiera de los trinomios factorizables, incluyendo binomios de la forma: X² – B². Por ejemplo: x² – 81 = 0, el que se factoriza en producto de suma por diferencia: (x + 9)• (x – 9) = 0, determinando las soluciones x₁ = -9 y x₂ = 9.

2. Utilizando la fórmula 
Todas las ecuaciones cuadráticas: ax² + b x + c = 0   (con a ? 0) Se pueden resolver utilizando la   fórmula:

Ejemplo: 
Resolver la ecuación   x² – 10x + 24 = 0 
En esta ecuación: a = 1; b = -10 y c = 24. Reemplazando en la fórmula, obtenemos: 

determinando así las soluciones   x₁ = 6 o x₂ = 4

Las “raíces o ceros” de una función son los valores de “x” para los cuales  f(x)=0

Como vimos, la expresión general de una función cuadrática es:

Las soluciones (raíces o ceros) de esta ecuación pueden calcularse mediante:

 

https://sites.google.com/site/e392funcion/home/ceros

Inecuaciones cuadráticas

 

https://www.vitutor.net/2/9/inecuaciones_cuadraticas.html

BLOQUES DE ALGEBRA Y GEOMETRIA

4. Vectores geométricos en el plano

Longitud y dirección, operaciones, aplicaciones a la geometría

En un sistema de ejes cartesianos, cada punto se describe mediante sus coordenadas.

Dados los puntos A y B, la flecha que va de A a B se llama vector, se representa por A Y B. A es el origen del vector y B el extremo.

Para calcular las coordenadas del vector AB, se restan las coordenadas del extremo menos las del origen.

Si el origen del vector es el origen de coordenadas (0,0), las coordenadas del extremo son las coordenadas del vector.

Un vector es un segmento orientado que va del punto A (origen) al punto B (extremo).

Todo vector se compone de un módulo, una dirección y un sentido.

Dirección de un vector

Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Sentido de un vector

El sentido del vector AB es que va del origen A al extremo B.

Módulo de un vector

El módulo del vector AB longitud del segmento AB, se representa por AB.

El módulo de un vector es un número siempre positivo o cero.

 

Matematicas Discretas

5. PROGRAMACION LINEAL

La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.

Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.

 

CONJUNTO FACTIBLE

El conjunto intersección, de todos los semiplanos formados por las restricciones, determina un recinto, acotado o no, que recibe el nombre de región de validez o zona de soluciones factibles.

 

 

OPTIMIZACIÓN DE FUNCIONES LINEALES SUJETAS A RESTRICCIONES (MÉTODO GRÁFICO).

 

OPTIMIZACIÓN DE FUNCIONES LINEALES

 

En el caso más simple, un problema de optimización consiste en maximizar o minimizar una función real eligiendo sistemáticamente valores de entrada (tomados de un conjunto permitido) y computando el valor de la función. La generalización de la teoría de la optimización y técnicas para otras formulaciones comprende un área grande de las matemáticas aplicadas. De forma general, la optimización incluye el descubrimiento de los "mejores valores" de alguna función objetivo dado un dominio definido, incluyendo una variedad de diferentes tipos de funciones objetivo y diferentes tipos de dominios.

f(x,y) = ax + by.

un problema de optimización puede ser representado de la siguiente forma

Dada: una función f : A  R donde A es un conjunto de números reales.

Buscar: un elemento x₀ en A tal que f(x₀) ≤ f(x) para todo x en A ("minimización") o tal que f(x₀) ≥ f(x) para todo x en A ("maximización").

 

BLOQUE DE ESTADISTICA Y PROBABILIDAD

6. PROBABILIDAD

FRECUENCIA

En estadística se pueden distinguir hasta cuatro tipos de frecuencias:

·         Frecuencia absoluta.- Es el promedio de una suma predeterminada y además consiste en saber cuál es el número o símbolo de mayor equivalencia. (n_i) de una variable estadística X_i, es el número de veces que este valor aparece en el estudio. A mayor tamaño de la muestra aumentará el tamaño de la frecuencia absoluta; es decir, la suma total de todas las frecuencias absolutas debe dar el total de la muestra estudiada (N).

·         Frecuencia relativa (f_i),.- Es el cociente entre la frecuencia absoluta y el tamaño de la muestra (N). 

           

 

siendo el f_i para todo el conjunto i. Se presenta en una tabla o nube de puntos en una distribución de frecuencias.

Si multiplicamos la frecuencia relativa por 100 obtendremos el porcentaje o tanto por ciento (p_i)

·        Frecuencia absoluta acumulada (N_i),.- Es el número de veces n_i en la muestra N.

·        Frecuencia relativa acumulada (F_i),.- Es el cociente entre la frecuencia absoluta acumulada

                                       

 

Supongamos que las calificaciones de un alumno de secundaria fueran las siguientes:

18, 13, 12, 14, 11, 08, 12, 15, 05, 20, 18, 14, 15, 11, 10, 10, 11, 13. Entonces:

·         La frecuencia absoluta de 11 es 3, pues 11 aparece 3 veces.

·         La frecuencia relativa de 11 es 0.17, porque corresponde a la división 3/18.

 

REPRESENTACION GRAFICA

 

Una gráfica es la representación en unos ejes de coordenadas de los pares ordenados de una tabla.

Las gráficas describen relaciones entre dos variables.

La variable que se representa en el eje horizontal se llama variable independiente o variable x.

La que se representa en el eje vertical se llama variable dependiente o variable y.

La variable y está en función de la variable x.

Una vez realizada la gráfica podemos estudiarla, analizarla y extraer conclusiones.

Para interpretar una gráfica, hemos de observarla de izquierda a derecha, analizando cómo varía la variable dependiente, y, al aumentar la variable independiente, x.

 

Kg de papas	2	4	6	8	10
Precio en Cntv	4	8	12	16	20

 

 

 

 

En esa gráfica podemos observar que a medida que compramos más kilos de papas el precio se va incrementando.

PROBABILIDAD

 

La probabilidad de un acontecimiento es un número, entendido entre 0 y 1, que indica las posibilidades que tiene de verificar cuando se realiza un experimento aleatorio.

 

SUCESO

 

Es cada uno de los resultados posibles de una experiencia aleatoria.

Al lanzar una moneda salga cara.

Al lanzar una moneda se obtenga 4.

 

SUCESO ALEATORIO

 

Es cualquier subconjunto del espacio muestral.

 

Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.

 

EJEMPLO

 

Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:

 

1. El espacio muestral.

E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}

2. El suceso A = {extraer tres bolas del mismo color}.

A = {(b,b,b); (n, n,n)}

3. El suceso B = {extraer al menos una bola blanca}.

B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}

4. El suceso C = {extraer una sola bola negra}.

C = {(b,b,n); (b,n,b); (n,b,b)}

TECNICA DE CONTEO

El principio fundamental en el proceso de contar ofrece un método general para contar el número de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

 

Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento B puede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a  n1 x n2.
 

¿De cuántas maneras pueden repartirse 3 premios a un conjunto de 10 personas, suponiendo que cada persona no puede obtener más de un premio?

Aplicando el principio fundamental del conteo, tenemos 10 personas que pueden recibir el primer premio. Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo, y posteriormente quedarán 8 personas para el tercer premio. De ahí que el número de maneras distintas de repartir los tres premios.

 

 

n

10 x 9 x 8 = 720

¿Cuántas placas de automóvil se pueden hacer utilizando dos letras seguidas de tres cifras? No se admiten repeticiones.

 

26 x 25 x 10 x 9 x 8 = 468000

 

n un número entero positivo, el producto n (n-1) (n-2)...3 x 2 x 1 se llama factorial de n.

El símbolo! se lee factorial y es el producto resultante de todos los enteros positivos de 1 a n; es decir, sea 

n

5! = 5 x 4 x 3 x 2 x 1 = 120

Por definición 0! = 1

 

 Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.

Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.

 

 Para facilitar el conteo examinaremos tres técnicas:

 

* La técnica de la multiplicación

* La técnica aditiva
* La técnica de la suma o Adición

* La técnica de la permutación

* La técnica de la combinación. 

 

ESPACIO DE PROBANILIDAD FINITO

 

Sea  d el espacio muestral, que contiene n elementos {a₁, a₂, a₃,.....,a_n}, si a cada uno de los elementos de d le asignamos una probabilidad p_i ³ 0, entonces estamos transformando este espacio muestral en un espacio finito de probabilidad; el que debe cumplir con las siguientes características:

 

1)    Las probabilidades asociadas a cada uno de los elementos de d deben ser mayores o iguales a cero, p_i³0.

2)    La sumatoria de las probabilidades asociadas a cada uno de los elementos de d debe de ser igual a 1.

Sp_i = 1

 

 

EJEMPLOS:

 

1.- Se lanza al aire un dado normal, si la probabilidad de que aparezca una de sus caras es proporcional al número que ostenta, a) ¿cuál es la probabilidad de que aparezca un número par?, b) ¿cuál es la probabilidad de que aparezca un número primo?

 

Solución:

 

                        d = {1, 2, 3, 4, 5, 6}

 

En este caso asignaremos las probabilidades como sigue;

 

p(aparezca el número 1) = p,  p(aparezca el número 2) = 2p, .....,

p(aparezca el número 5) = 5p, p(aparezca el número 6) = 6p

Y por ser d un espacio finito de probabilidad, entonces,

 

p(d) = p + 2p +  3p + 4p + 5p + 6p =1

 

Por tanto,   21p = 1, luego,  p = 1/21

 

a.       Luego;

 

A = evento de que aparezca un número par = {2, 4, 6}

 

p(A)=p(2)+p(4) + p(6) = 2p + 4p + 6p = 12p = 12(1/21) = 12/21= 0.5714

b.      B = es el evento de que aparezca un número primo = {1, 2, 3, 5}

p(B)=p(1) + p(2) + p(3) + p(5) = p + 2p + 3p + 5p = 11p = 11(1/21) = 11/21 =                      0.5238

 

 

DEFINICIÓN DE ESTADÍSTICA

La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

Un estudio estadístico consta de las siguientes fases:

• Recogida de datos.
• Organización y representación de datos.
• Análisis de datos.
• Obtención de conclusiones.

CONCEPTOS DE ESTADÍSTICA

POBLACIÓN

Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.

INDIVIDUO

Un individuo o unidad estadística es cada uno de los elementos que componen la población.

MUESTRA

Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.

MUESTREO

El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.

VALOR

Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.

DATO

Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz.