MATEMÁTICAS 2

 

Función

En matemáticas, se dice que una magnitud es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r². Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, T = d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.

En algebra abstracta, el concepto general de función, aplicación o mapeo se refiere en a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto. Por ejemplo, cada numero entero posee un único cuadrado, que resulta ser un número natural:

...	−2 → +4,	−1 → +1,	±0 → ±0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:

...,

Estación → E,

Museo → M,

Arroyo → A,

Rosa → R,

Avión → A,

...

 

 

Función monótona 

 

Sea

F: P--------> Q

Una funcion entre dos conjuntos P y Q, donde cada conjunto tiene un orden parcial (los dos se denotarán por ≤). En cálculo se habla de funciones entre subconjuntos de los reales, y el orden ≤ no es otro que el orden usual de la recta real, aunque esto no es esencial para la definición.

La función f es monótona si y solo si x ≤ y implica f(x) ≤ f(y) (es decir, la función es creciente), o bien x ≤ y implica f(x) ≥ f(y) (es decir, la función es decreciente). En otras palabras, una función es monótona si conserva el orden.

Monotonía  en cálculos y análisis 

En cálculo no hay usualmente necesidad de invocar los métodos abstractos de la teoría del orden. Como ya se señaló, las funciones se establecen entre (subconjuntos de) números reales, ordenados de forma natural.

Por la forma de la grafica de una función monótona en los reales, tales funciones se llaman también monótonamente crecientes (o no decreciente), respectivamente.

Ejemplo gráfico

A continuación se muestran tres gráficas de funciones cualesquiera. La primera de ellas es una función estrictamente creciente por la izquierda y por la derecha, mientras que es constante en el medio; por lo demás, es creciente pues conserva el orden ascendente durante todo el recorrido de la función. La segunda de ellas es estrictamente decreciente por la izquierda y por la derecha, puesto que conserva el orden descendente durante todo el recorrido de la función. La última de ellas es una función con un recorrido con partes donde la función es creciente y partes donde es decreciente (presenta máximos y mínimos relativos).

Función monótona creciente.

Función monótona decreciente.

Función no monótona.

 

 

 

Aplicaciones y resultados

Monotonía En matemáticas, cada una de las siguientes propiedades de una función f: R → R implica la siguiente:

f es monótona.

f tiene un límite por la izquierda y por la derecha en cualquier punto de su dominio de definición.

f sólo puede tener discontinuidades de salto.

f sólo puede tener una cantidad enumerarle de discontinuidades.

Estas propiedades son la razón por la que las funciones monótonas son útiles en el análisis matemático. Dos importantes hechos que se deducen que una función sea monótona son:

• Si f es una función monótona definida en un intervalo I, entonces f es derivable casi siempre en I, es decir, el conjunto de puntos x en I en donde f no es diferenciable tiene medida de Lebesgue 0.
• Si f es una función monótona definida en un intervalo [a, b], entonces f es Riemann-integrable.
• Una importante aplicación de las funciones monótonas es en probabilidad. Si X es una variable aleatoria, su función de distribución
• FX(X)=P(X

Es una función creciente

 

Simetría

Respecto del eje de ordenadas

Una función f es simétrica respecto del eje de ordenadas si ésta es una función par, es decir:

f(-x) = f(x)

 f(x)=x⁴-3x²+4

f(-x)=(-x⁴)-3(-x)²+4=x⁴-3x²+4=f(x)

Simetría respecto al origen

Una función f es simétrica respecto al origen si ésta es una función impar, es decir:

f(-x) = -f(x)

f(x)=x⁵-3x³

f(-x)=(-x)⁵-3(-x)³ =-x⁵+3x³=-(x⁵-3x³)=-f(x)

 

 

Clasificación de funciones

Funciones algebraicas

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas

Si se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x − 2

Funciones implícitas

Si no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x − y − 2 = 0

Funciones polinómicas

Son las funciones que vienen definidas por un polinomio.

f(x) = a₀ + a₁x + a₂x² + a₂x³ +··· + a_nxⁿ

Su dominio es , es decir, cualquier número real tiene imagen.

Funciones constantes

El criterio viene dado por un número real.

f(x)= k

La gráfica es una recta horizontal paralela a al eje de abscisas.

Funciones polinómica de primer grado

f(x) = mx +n

Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.

     Función afín.

     Función lineal.

     Función identidad.

     Funciones cuadráticas

f(x) = ax² + bx +c

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

Funciones a trozos

Son funciones definidas por distintos criterios, según los intervalos que se consideren.

 

Ø  Funciones en valor absoluto.

Ø  Función parte entera de x.

Ø  Función mantisa.

Ø  Función signo.

Funciones racionales

El criterio viene dado por un cociente entre polinomios:

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

Funciones radicales

El criterio viene dado por la variable x bajo el signo radical.

El dominio de una función irracional de índice impar es R.

El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.

Funciones trascendentes

La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

Función exponencial

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia a^x se llama función exponencial de base a y exponente x.

Funciones logarítmicas

La función logarítmica en base a es la función inversa de la exponencial en base a.

Funciones trigonométricas

Función seno

f(x) = sen x

Función coseno

f(x) = cos x

Función tangente

f(x) = tg x

Función cosecante

f(x) = cosec x

Función secante

f(x) = sec x

Función cotangente

f(x) = cotg x

 Paridad de las funciones.

 

En matemáticas, se puede clasificar a las funciones según su paridad: Las funciones pueden ser pares, impares o no tener paridad.

Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares de simetría, con respecto a sus funciones inversas aditivas (funciones inversas aditivas u opuestas son funciones que al sumarlas el resultado es cero).

Función par:

 

 F(-x) =f(x)

 

Función impar:

f (-x)=-f(x)

 

 Propiedades de las funciones pares e impares:

- La única función que es tanto par e impar es la función cero (f(x) = 0 para todo x).

- La suma de una función par y una impar no es ni par ni impar, a menos de que una de las funciones sea el cero.

- La suma de dos funciones par es una función par, y todo múltiplo de una función par es una función par.

- La suma de dos funciones impares es una función impar, y todo múltiplo constante de una función impar es una función impar.

- El producto de dos funciones pares es una función par.

- El producto de dos funciones impares es una función par.

- El producto de una función par y una función impar es una función impar.

- El cociente de dos funciones pares es una función par.

- El cociente de dos funciones impares es una función par.

- El cociente de una función par y una función impar es u

- La derivada de una función par es una función impar.

-La derivada de una función impar es una función par

 

Integrales de funciones pares e impares

-          La integral de una función impares entre –A y+A es cero ( donde la función no posee ninguna asíntota vertical entre –A y A)

 

 

-          LA intergral de una función par entre –A y +Aes el doble de la integral entre 0 y +A( la función no posee ninguna asíntota vertical entre –A y A)

 

Funciones racionales

El criterio viene dado por un cociente entre polinomios:

 

El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.

Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:

Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones.   

 

 

Funciones trigonométricas

Función seno

f(x) = sen x

Dominio: R

Recorrido: [−1, 1]

Período: 2π rad

Continuidad: Continua en 

Impar: sen(−x) = −sen x

 

f(x) = cos x

Dominio: R

Recorrido: [−1, 1]

Período: 2π rad

Continuidad: Continua en 

Par: cos(−x) = cos x

 

Función tangente

f(x) = tg x

Dominio: 

Recorrido: R

Continuidad: Continua en Período: 

Impar: tg(−x) = −tg x

 

Función cotangente

f(x) = cotg x

Dominio:

Recorrido: R

Continuidad: Continua en 

Período: 

Impar: cotg(−x) = −cotg x

 

Función secante

f(x) = sec x

Dominio: Recorrido: (− ∞, −1]  [1, ∞)

Período: 2π rad

Continuidad: Continua en 

Par: sec(−x) = sec x

Función cosecante

f(x) = cosec x

Dominio: 

Recorrido: (− ∞, −1]  [1, ∞)

Período: 2π rad

Continuidad: Continua en 

Impar: cosec(−x) = −cosec x

 

La función cuadrática

Una función cuadrática es aquella que puede escribirse de la forma: 

f(x) = ax2 + bx + c

donde a, b y c son números reales cualesquiera y a distinto de cero.

Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.

Como ejemplo, ahí tienes la representación gráfica de dos funciones cuadráticas muy sencillas:

f(x) = x2

f(x) = -x2

Obtención del vértice de una parábola

El vértice de una parábola está situado en el eje de ésta y, por tanto, su abscisa será el punto medio de las abscisas de dos puntos de la parábola que sean simétricos.
Como toda función cuadrática pasa por el punto (0,c) y el simétrico de éste tiene de abscisa x = -b/a, la del vértice será Xv = -b/2a. La ordenada Yv se calcula sustituyendo el valor de Xv en la ecuación de la función.

Intersección de la parábola con los ejes

Intersección con el eje OY: Como todos los puntos de este eje tienen la abscisa x = 0, el punto de corte de la parábola con el eje OY tendrá de coordenadas (0,c) 

Intersección con el eje OX: Como todos los puntos del eje OX tienen la ordenada y = 0, para ver estos puntos de corte se resuelve la ecuación de segundo grado ax2 + bx + c = 0.

Dependiendo del valor del discriminante (D) de la ecuación, se pueden presentar tres situaciones distintas:

Si D > 0, la ecuación tiene dos soluciones reales y distintas y la parábola cortará al eje OX en dos puntos.

Si D = 0, la ecuación tiene una solución real y, por tanto, la parábola cortará al eje OX en un punto (que será el vértice).

Si D < 0, la ecuación no tiene soluciones reales yla parábola no cortará al eje OX.

Cálculo de puntos de la parábola

Podemos hallar los puntos de la parábola que necesitemos sin más que sustituir, en la ecuación de la función cuadrática, la variable x por aquellos valores que deseemos.

Toda función cuadrática f(x) = ax2 + bx + c, representa una parábola tal que:

Su forma depende exclusivamente del coeficiente a de x2.

Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.

Si a > 0, las ramas van hacia arriba y si a < 0, hacia abajo.

Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.

Existe un único punto de corte con el eje OY, que es el (0,c)

Los cortes con el eje OX se obtienen resolviendo la ecuación ax2 + bx + c=0, pudiendo ocurrir que lo corte en dos puntos, en uno o en ninguno.

La primera coordenada del vértice es Xv = -b/2a.

Ejemplo

Ejercicio

• ¿Cómo describirías la

función?:

f(x) = 2(x+2)²- 1                                                                                             

Respuesta:

Al multiplicarse por positivo 2, será más  estrecha y será cóncava hacia arriba, al  sumarse dos dentro del paréntesis, se mueve  dos veces hacia la izquierda y al restarle 1 a la  función, bajará una unidad.

 

La forma estándar de la  función cuadrática

• Una función cuadrática en la forma de

f(x) = ax²+ bx + c

• Se puede escribir en la forma estándar:

f(x) = a(x-h)²+ k, donde (h,k)

Representan el vértice de la función.

¿Cómo convertir una función cuadrática en su forma  estándar?

• Sea f(x) = 2x²+ 8x + 7

• Escríbela en su forma estándar

Pasos:

1.   Escojamos los primeros dos términos para completar el cuadrado.

f(x) = (2x² + 8x) + 7

2. Sacamos el dos como factor común

f(x) = 2(x² + 4x) + 7

 

3. Completamos el cuadrado

f(x) = 2(x² + 4x + 4 – 4) + 7

4.   Factorizamos y sumamos

f(x) = 2(x + 2)² + 7 - 8

5. Forma estándar f(x) = 2(x +  2)² -1

Repetición del ejercicio

• f(x) = 2x²+ 8x + 7   función cuadrática

f(x) = (2x²+ 8x) + 7 Escoges los primeros dos términos  para completar el cuadrado

f(x) = 2(x²+ 4x) + 7 Sacas el dos como factor  común

f(x) = 2(x²+ 4x + 4 – 4) + 7 Completas el cuadrado

f(x) = 2(x + 2)²+ 7 – 8 Factorizas y restas el número  añadido

f(x) = 2(x + 2)²- 1 Ya está en su forma estándarTrata los siguientes  ejercicios

• Escribe la siguiente función cuadrática como una función  estándar:

1. f(x) = -x² + 6x – 8                                        1. f(x) = -(x – 3)²+ 1

2. f(x) = x² - 8x + 16                                        2.   f(x) = (x – 4)²

3. g(x) = 2x² + 16x + 11                                  3.    f(x) = 2(x + 4)²- 21

 

Los interceptos de las  funciones cuadráticas

• Encontramos los interceptos en x  cuando la gráfica pasa por el eje de  de x.

• Para hallar los interceptos en x,  igualamos la función a cero.

• Ejemplo:

– Halla los interceptos de la siguiente función:    f(x)= x²-9x + 18

Solución

• f(x)= x²-9x + 18

1. Halla los interceptos  en Y (iguala la x=0)

f(0)= 0²-9(0) + 18

(0, 18)

Intercepto en y

2.  Halla los interceptos en x:  (igualar la función  a cero)  f(x) = 0   x²-9x + 18 = 0

Factorzas: (x-3)(x-6) = 0

X=3 ;  x=6

(3, 0) y (6, 0)

Hallar el vértice

Recuerda completar el  cuadrado:

F(x) = x²-9x + 18

(x²-9x) + 18

(x²-9x + 20.25 – 20.25) + 18

(x – 4.5)²+ 18 – 20.25

(x – 4.5)²– 2.25

 

Gráfica

Cuando tenemos los interceptos y el vértice, ya se

puede trazar la gráfica

  

Otra manera de obtener el vértice de una función cuadrática

• Utiliza la formula

X=  -  b    

         2 a

Sea f(x) = x² - 9x + 18

a =1,   b = -9

Sustituyes los valores en la fórmula y luego evalúas la función  con el resultados de x

 

 

Funciones pares e impares

Funciones pares:

1. Si es simétrica con

el eje de y

 

                                                2.   Si f(-x) = f(x)

Funciones impares

1. Si es simétrica con

el origen.

                                                2. Si f(-x) = -f(x)

 

Prueba si las siguientes funciones son pares, impares o  ninguna

 

• Para determinar si es par, sustituimos el valor de x por –x y nos vuelve a dar la función original es par y si es impar nos dará el opuesto de la función:

– Ejemplo:

• F(x) = x⁵ + x

F(-x)= (-x)⁵ + (-x)

F(-x) = -x⁵ - x

F(-x)= -(x⁵ + x) por tanto es impar porque f(-x) = -f(x)

Polinomios

UNIDAD 5 – Polinomios

Introducción

Con el álgebra se pasa del número al símbolo, de lo particular a lo general. La gran  expresividad del lenguaje algebraico facilita la obtención de relaciones, propiedades y la  resolución de problemas.

Para trabajar eficazmente en matemática se debe operar convenientemente con  expresiones algebraicas de forma tal que se puedan transformar en otras expresiones  equivalentes más fáciles de manejar.

Además, en Ingeniería, al realizar el modelado matemático de un problema, es frecuente  obtener un polinomio. Para encontrar la solución de la situación planteada es necesario  conocer las “raíces” de dicho polinomio. 

5.1.- Expresiones algebraicas

Se llama expresión algebraica a cualquier combinación de números representados por letras  o por letras y cifras, vinculados entre sí por las operaciones de suma, resta, multiplicación,  división, potenciación y radicación.

Son ejemplos de expresiones algebraicas:

 

En este curso se considerarán expresiones algebraicas en las que intervengan solamente  números reales.

 5.1.1.- Clasificación de las expresiones algebraicas

 

FUNCIONES POLINÓMICAS

 

Introducción

Después de haber trabajado con rectas y con parábolas vamos a estudiar otras funciones de la misma familia, cuya fórmula es un polinomio.

Las principales características es que se trata de funciones definidas para cualquier número "real" y continuas.

En las siguientes actividades queremos que identifiques el tipo de gráfica de una función polinómica según su GRADO. Para ello debes identificar las siguientes características:

- Número de puntos de corte con el eje OX

- Intervalos de crecimiento y de decrecimiento.

- Número de puntos máximos y míninos.

La función constante

FUNCIÓN POLINÓMICA DE GRADO 0

y = k

1.- ¿Corta en algún punto al eje OX?

2.- ¿Qué características tienen todas las rectas que representan funciones constantes?

 

La función afin: FUNCIÓN POLINÓMICA DE GRADO 1

Se denomina función afin a toda función de la forma:

y = m * x + k

Donde m (distinto de 0) y k son números reales.

Modifica los parámetros m y k para observar cómo influye cada uno de ellos en la gráfica.

3. ¿Cuántos puntos de corte tiene con el eje OX?

4. ¿Qué características tienen todas las rectas que representan funciones afines? Indicar los intervalos de crecimiento o decrecimiento según los valores de m.

 La función cuadrática:

FUNCIÓN POLINÓMICA DE GRADO 2

Se denomina función cuadrática a toda función de la forma:

y=a*x2+b*x+c

donde a (distinto de 0), b y c son números reales.

Cualquier función de esa forma es una parábola.

Modifica los parámetros a, b y c para observar cómo influye cada uno de ellos en la gráfica.

5.- Escribe la fórmula de tres parábolas con 0, 1 y 2 puntos de corte con el eje OX respectivamente.

6.- ¿Qué características tienen todas las parábolas que representan funciones cuadráticas?

7.- Indicar los intervalos de crecimiento o decrecimiento, y los máximos o mínimos de las tres parábolas del apartado 5.

8.- ¿En qué casos una función cuadrática sólo tiene 1 punto de corte con el eje OX? ¿De qué punto se trata?

 

La función cúbica:

FUNCIÓN POLINÓMICA DE GRADO 3

Se denomina función cúbica a toda función de la forma:

y=a*x3+b*x2+c*x+d

donde a (distinto de 0), b, c y d son números reales.

La gráfica de la pantalla corresponde a la función:

y = x3- 3x2 + 3

9.- Modifica el parámetro d para observar cómo influye en la gráfica. (Recuerda que para volver a la función anterior debes utilizar inicio)

- Escribe la fórmula de tres funciones cúbicas que tengan 3, 2 y 1 punto de corte con el eje OX, respectivamente. ¿En cuántos puntos alcanzan las funciones un máximo o un mínimo? Indica los intervalos de crecimiento y de decrecimiento.

- ¿Cómo son los puntos de corte con el eje OX cuando sólo hay 2?

- ¿Puede una función cúbica no tener ningún punto de corte con el eje OX?

10.- Modifica los parámetros a, b y c para observar cómo influye cada uno de ellos en la gráfica:

- Representa funciones de la forma y = a*x3 e indica sus características principales (puntos de corte con el eje OX, crecimiento-decrecimiento, puntos máximos-mínimos).

- ¿Cuál es el número de puntos de corte con el eje OX que puede tener una función cúbica?

- ¿Existen funciones cúbicas con un sólo punto máximo o mínimo? ¿Y con ninguno?

 FUNCIÓN POLINÓMICA DE GRADO 4

Es la función de fórmula: y=a*x4+b*x3+c*x2+dx+e

donde a (distinto de 0), b, c, d y e son números reales.

Modifica los parámetros a, b, c, d y e para observar como influye cada uno de ellos en la gráfica.

11.- Para cada uno de los siguientes supuestos, escribe la fórmula de una función de grado 4 que cumpla las condiciones:

- No tenga ningún punto de corte con el eje OX y tenga dos mínimos y un máximo.

- Un punto de corte con el eje OX y dos máximos y un mínimo.

- Dos puntos de corte con el eje OX y un sólo mínimo.

- Tres puntos de corte con el eje OX. ¿Cuántos máximos o mínimos tiene necesariamente?

 

El algoritmo de Euclides

El algoritmo de Euclides es un procedimiento para calcular el m. c. d. de dos números. Los pasos son:

1. Se divide el número mayor entre el menor.

2. Si:

1. La división es exacta, el divisor es el m. c. d.

2. La división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m. c. d.

Calcular el m.c.d. de:

72 y 16

 

m. c. d. (72, 16) = 8

El máximo común divisor de dos enteros puede obtenerse escogiendo el mayor de todos los divisores comunes. Hay un proceso más eficiente que utiliza repetidamente el algoritmo de la división. Este método se llama algoritmo de Euclides. 

El algoritmo de Euclides se describe de la forma siguiente: Dados dos enteros a y b cuyo máximo común divisor se desea hallar, y asumiendo que a b > 0, (El método funciona también si a y b son negativos). Basta trabajar con los valores absolutos de estos números, debido a que M.C.D (|a|, |b|) =M.C.D (a,b) se siguen los siguientes pasos:

a) Se usa el algoritmo de la división para obtener a = q₁b + r₂ con 
0 £ r₁ < b.  Si  r₁ = 0, entonces bïa y M.C.D.(a, b) = b.

b) Si r₁ ¹ 0 se divide b por r₁ y se producen enteros q₂y r₂ que satisfacen b =q₂ r₁ + r₂  con 0 £ r₂ < r₁. Si r₂ = 0 el proceso termina y M.C.D.(a, b) = r_1.

c) Si r₂ ¹ 0 se procede a dividir r₂ por r₁ obteniendo r₁ = q₃ r_{2 +} r₃  con 0 £  r₃ < r_2.

d) Este proceso continua hasta que algún residuo cero aparece. Esto ocurre porque en la secuencia  b > r₁ >  r₂  >  .....   ³ 0  no puede haber más de b enteros. Es decir, el proceso es finito.

e) En estas circunstancias, el máximo común divisor de a y b no es más que el último residuo no cero del proceso anterior.

Esto lo garantiza la aplicación reiterada del siguiente teorema 

 Definición. El término ecuación diofántica se usa para designar una ecuación en una o más incógnitas que va a ser resuelta en los enteros. La ecuación diofántica más simple es la ecuación diofántica lineal en dos incógnitas ax + by = c donde a y b son enteros dados no ambos cero. 
 Ejemplo 32.

La ecuación diofántica  3x + 6y = 18 tiene infinitas soluciones enteras. Algunas de estas soluciones son:

x =  4,       y=1

x = 6,        y=6

x = 10,      y=-2

  

Ejemplo 33.

La ecuación diofántica 2x + 10y = 17 no posee solución debido a que tanto 2x como 10y= 17 como son números pares. La suma de dos números pares es un número par y 17 es un número impar. 
 

Un criterio para conocer cuando una ecuación diofántica de este tipo posee solución lo proporciona el siguiente teorema. 

8.7.3 Teorema. La ecuación diofántica ax + by = c tiene solución sí y sólo sí dc, donde d = M.C.D.(a, b).

Si xo y yo es una solución particular de esta ecuación entonces todas las otras soluciones están dadas por: 

Ejemplo 34.

La ecuación 2x + 10y = 17  no tiene solución porque: 2 = M.C.D.(2, 10) no divide a 17. 
 

Ejemplo 35.

La ecuación 5x + 6y = 8  tiene solución porque: 1 = M.C.D.(5, 6) divide a 8.

¿Cómo hallamos una solución particular?

Existen dos métodos. El primero es por simple inspección, pero si así no fuera posible, podemos utilizar el algoritmo de Euclides así: 
 

1 = 5x + 6y   Se hallan x y y utilizando el algoritmo anteriormente citado.

6 = 15 + 1.

5 = 51 + 0.

Luego 1 = 6  15. Lo que quiere decir que 1 = 5x(-1)+6x(1). Entonces:
x = -1,  y = 1. 
 

En la expresión 5x(-1)+6x(1) = 1 se multiplican ambos miembros por 8 y se obtiene: 5x(-8)+6x(8) = 8.

Luego la solución particular de la ecuación diofántica es de la forma siguiente:
x0 = -8,   y0 = 8.

La solución general será: 
x = -8+6t,  y = 8-5t. 
 

8.7.4 Definición. Un entero p > 1 es llamado un número primo sí y sólo sí sus únicos divisores positivos son 1 y p. Un entero mayor que 1 que no es primo se llama compuesto. 
  

8.7.5 Teorema Fundamental de la Aritmética

Todo entero n > 1 puede ser expresado como producto de primos. Esta representación es única salvo el orden de los factores.

El teorema anterior garantiza que todo entero n puede escribir de forma única de la manera siguiente:

n = p1k1 p2k2 ....prkr, donde p1 p2 ... pn son primos y k1 k2 ... kr son enteros positivos

Se puede demostrar que si un entero n está escrito en la forma anterior, entonces el número de sus divisores positivos viene dado por: 

(n)= (k1+1) (k2+1)...(kr+1)

Resultados similares se pueden obtener en el caso que n sea negativo. 
  

Ejemplo 37.

1001 se puede escribir como producto de primos de forma única como 1001 = 7 x 11 x 13 . 
  

Ejemplo 38.

24 se puede escribir como producto de primos de forma única como 24 = 2  x 2 x 2 x 3, es decir, 24 = 23 x 3. 
 

Ejemplo 39.

El número de divisores de 1001 es: 
(1001) = (1+1)(1+1)(1+1) = 8 
 

Ejemplo 40.

El número de divisores de 24 es:
(24) = (3+1)(1+1) = 8 
 

Ejemplo 41.

1001 se puede escribir salvo el signo como producto de primos de forma única como 1001 =  (71113). 
 

Ejemplo 42.

El número de divisores positivos de 1001 es  (1001) = 8. 
 

8.7.6 Definición. El mínimo común múltiplo de dos enteros a y b ambos diferentes de cero, denotado por m.c.m.(a, b) es el entero positivo m que satisface:

i. a|n y b|m

ii. Si a|c y b|c con c>0, entonces m y c. 

Ejemplo 43.

Probar que un entero positivo n > 1 es cuadrado perfecto sí y sólo sí en su descomposición en factores primos todos los exponentes son pares.

Sea n = p1k1 p2k2 ....prkr, donde p1 p2 ... pr la descomposición en factores primos de n.

n es cuadrado perfecto sii existe un b  Z tal que b=(p1k1p2k2....prkr)1/2 sí y sólo sí ki/2  Z y esto sólo se dá si ki es par. 

Ejemplo 44.

Una compañía compró cierto número de reliquias falsas a $17 cada una y vendió algunas de ellas a $49 cada una. Si la cantidad comprada originalmente es mayor que 50 y menor que 100 y la compañía obtuvo una ganancia de $245. ¿Cuántas reliquias faltan por vender?

Sea x: número de reliquias que compró.

y: número de reliquias que vendió.

Se sabe que 50 < x < 100.

Lo que vendió menos lo que compró debe ser igual a la ganancia. Luego: 49y - 17x = 245. Se trata de resolver esta ecuación diofántica.

M.C.D.(17, 49) = ?. Utilicemos el algoritmo de Euclides.

49 = 2*17+15

17 = 1*15+2

15 = 7*2+1

7 = 7*1+0 
  
 

Luego M.C.D.(17, 49) = 1

Podemos decir, entonces, que: 1 = 15 - 7 x 2 

1 = 15 - 7 x (17-1x15)

1 = 8 x 15 -7 x 17

1 = 8 x (49 - 2 x 17) - 7 x 17

1 = 8 x 49 -23 x 7

O sea que: 49 x 8 -17 x 23 = 1. Multiplicando por 245 obtenemos:

49 x 1960 -17 x 5635 = 245

Así que una solución particular de la ecuación diofántica 49y - 17x = 245 es y0 = 1960; x0 = 5635.

La solución general para  x es: x = 5635 + 49t

Bajo las condiciones del problema, sólo se obtiene que con  t = -113 se cumple que x = 98, o sea que compró 98 reliquias.

Para t = -113 se tiene que  y = 1960 + 17t da como resultado  y = 39 que fueron las reliquias que vendió. Luego faltan por vender 59 reliquias. 

Modelo

Un modelo matemático se define como una descripción desde el punto de vista de las matemáticas de un hecho o fenómeno del mundo real, desde el tamaño de la población, hasta fenómenos físicos como la velocidad, aceleración o densidad. El objetivo del modelo matemático es entender ampliamente el fenómeno y tal vez predecir su comportamiento en el futuro.
El proceso para elaborar un modelo matemático es el siguiente:

Encontrar un problema del mundo real

Formular un modelo matemático acerca del problema, identificando variables (dependientes e independientes) y estableciendo hipótesis lo suficientemente simples para tratarse de manera matemática.

Aplicar los conocimientos matemáticos que se posee para llegar a conclusiones matemáticas.

Comparar los datos obtenidos como predicciones con datos reales. Si los datos son diferentes, se reinicia el proceso.

2. Modelos Lineales

Se dice que una función es lineal cuando su gráfica es una línea recta; y por consecuencia tiene la forma:
y = f(x) = mx + b
Donde m representa la pendiente de la recta y b la ordenada al origen (el punto en el que la recta interfecta al eje de las "y"). Es importante mencionar que este tipo de funciones crecen a tasa constante; y su dominio e imagen son todos los números reales.

 

Circulo trigonométrico

Círculo trigonométrico. También conocido como goniométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad. El círculo trigonométrico tiene la ventaja de ser una herramienta práctica en el manejo de los conceptos de trigonometría, pero al mismo tiempo es un apoyo teórico, pues ayuda a fundamentar y tener una idea precisa y formal de las funciones trigonométricas. Atreves del círculo trigonométrico se puede obtener de forma manual o analítica el valor aproximado de las razones trigonométricaspara un ángulo determinado si se dispone de los instrumentos geométricos necesarios.

RAZONES TRIGONOMETRICA

Si se rota la semirrecta OP de radio r rota hasta formar un ángulo α, si proyectamos el punto P hasta el eje X,Y, se obtienen dos segmentos; sobre el eje Y se proyecta el segmento OB denominado seno del ángulo α (Seno α), sobre el eje X se proyecta el segmento OA denominado coseno del ángulo α (cos α), formando un triángulo rectángulo OAP, cuyo lado AP se le denomina cateto opuesto al ánguloα, el lado OA es el cateto adyacente al ángulo α, mientras que el lado OP= r se denomina hipotenusa. Del triángulo rectángulo anterior podemos denotar las razones trigonométricas siguientes:

sen α = PA/r

cos α = OA/r

tang α = PA/OA

cot α= OA/PA

Seno del ángulo α

A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hacia el eje Y se obtiene un segmento OB = AP que se denomina seno del ángulo α (se denota como sen α), también se determina a través de la razón (PA/r).\

 

Coseno del ángulo α

A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hasta el eje X se obtiene un segmento OA = BP que se denomina coseno del ángulo α (se denota como cos α), también se determina a través de la razón OA/r

Tangente del ángulo α

Si trazamos una semirrecta EC tangente a la circunferencia por el punto E, que toque la semirrecta OD (prolongación de la semirrecta r), se forma el segmento EC que se denomina tangente del ángulo α(se denota con tang α); también se determina a través de la razón PA/OA.

Cotangente del ángulo α

Si trazamos una semirrecta FD, tangente al punto F y que toque la semirrecta OD, se forma un segmento FD denominado Cotangente del ángulo α (cot α); ); también se determina a través de la razónOA/PA.

Cuadrantes del círculo trigonométrico

Si dividimos el círculo trigonométrico en 4 partes iguales se obtiene como resultado que cada [ángulo] consecutivo mide 90° (π/2 rd), cada una de las partes obtenidas se conoce como cuadrantes del círculo trigonométrico. En cada cuadrante los parámetros seno, coseno, tangente y cotangente cambian su valor numérico con el aumento o disminución del ángulo α, este hecho lo corrobora las razones trigonométricas anteriores.

Primer cuadrante

 

Parámetro Signo Seno + Coseno + Tangente + Cotangente +

En el primer cuadrante (QI), con el aumento del [ángulo] α, disminuye el cos α y la cot α, mientras que aumenta la tang α y el sen α, hasta alcanzar su máximo o mínimo valor a 90° (π/2).

Segundo cuadrante

Parámetro Signo Seno + Coseno - Tangente - Cotangente -

 

En el segundo cuadrante, con el aumento del ángulo α, disminuyen el sen α y el cos α, por lo que lo hacen también tang α y cot α, alcanzando su mínimo valor a 180° (πrd).

Tercer cuadrante

 

Parámetro Signo Seno - Coseno - Tangente + Cotangente +

En el tercer cuadrante (QIII), con el aumento del ángulo α, disminuyen el senα y el cosα, la tangα aumenta su valor, mientras que la cotα disminuye dado que (a partir de que seno y el coseno son negativos y la relación existente entre ellos) hasta alcanzar su mínimo o máximo valor a 270° (3π/2).

 

 

 

Cuarto cuadrante

 

 

Parámetro Signo Seno - Coseno + Tangente - Cotangente -

En el cuarto cuadrante (Q IV), con el aumento del ángulo α, dirminuye el sen α , mientras que aumenta el cos α por lo que aumenta la cotα , mientras que disminuye la tangα y el, hasta alcanzar su máximo y mínimo valor a 360° (π rd).

Dominio y recorrido de funciones polinómicas

Dominio

El dominio de una función polinómica son todos los números reales. Se expresa como Dom f(x)= ℜ.

No tenemos que calcular nada.

La función existe desde x = - ∞ hasta x = + ∞.

El dominio también se puede expresar así: Dom f(x)= (- ∞, + ∞)

Son funciones polinómicas las rectas, las funciones cuadráticas (parábolas) y las funciones polinómicas de grado superior

PARIDAD

En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del orden. Aunque los conceptos generalmente coinciden, las dos disciplinas han desarrollado una terminología ligeramente diferente; mientras en cálculo se habla de funciones monótonamente crecientes y monótonamente decrecientes (o simplemente crecientes y decrecientes), en la teoría del orden se usan los términos monótona y antítona, o se habla de funciones que conservan e invierten el orden.

(Presenta máximos y mínimos relativos).

Paridad

En matemáticas, se puede clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares de simetría, con respecto a inversas aditivas. Las funciones pares e impares son usadas en muchas áreas del análisis matemático, especialmente en la teoría de las series de potencias y series de Fourier. Deben su nombre a la paridad de las potencias de las funciones monómicas que coinciden y por tanto satisfacen las condiciones de paridad. Así, la función xn es una función par si n es un entero par o una función impar si n es un entero impar.

Funciones pares

 

 

Funciones impares                                                           

 

Una función impar es cualquier función que satisface la relación:

para todo x en el dominio de f.

Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.

 

Identidades trigonométricas fundamentales

cos² α + sen² α = 1

sec² α = 1 + tg² α

cosec² α = 1 + cotg² α

 

 

 

 

Derivadas trigonométricas inversas

Derivada del arcoseno

 

Derivada del arcocoseno

 

Derivada del arcotangente

 

 

Ecuaciones trigonométricas

En las  ecuaciones trigonométricas intervienen funciones trigonométricas, que son periódicas y por tanto sus soluciones se pueden presentar en uno o en dos cuadrantes y además se repiten en todas las vueltas.

Para resolver una ecuación trigonométrica haremos las transformaciones necesarias para trabajar con una sola función trigonométrica, para ello utilizaremos las identidades trigonométricas fundamentales.

 

Función Compuesta

 Siempre que se tienen dos funciones g y f se puede definir una nueva función de manera que la variable dependiente de g sea a su vez la variable independiente de f. Observa la siguiente ilustración entre los conjuntos.

 

 

Método de Integración de Funciones Trigonométricas Compuestas

PARTE I: Recordatorio de fórmulas trigonométricas.

Las fórmulas que resultan imprescindibles son estas cuatro: sen (x+y), sen(x-y), cos(x+y) y cos(x-y). A partir de ellas se puede deducir el resto de fórmulas que son de mucha utilidad para resolver integrales de funciones trigonométricas compuestas. A continuación se expone una forma, que a mí me funciona, para recordarlas.
Se trata de deducirlas a partir de la fórmula de Euler de representación de números complejos. A partir de esta fórmula que enuncia que todo número complejo (z) de módulo 1 puede ser expresado mediante la notación:

z= 1 * [cos x + i sen x] = e^xi. Donde cos x es la PARTE REAL ysen x es la PARTE IMAGINARIA del número complejo.

Sabiendo que el producto de dos números complejos da como resultado otro número complejo cuyo módulo es el producto de los módulos y cuyo argumento es la suma de los argumentos, se puede deducir las funciones trigonométricas de la suma y resta de ángulos como el producto de dos números complejos de módulo 1 y argumento x e y respectivamente; tal que

e^xi * e^yi = e^(x+y), o bien, para la resta: e^xi * e^-yi = e^(x-y)i.

Esto, atención, NO DEMUESTRA la identidad matemática de la función trigonométrica de la suma o resta de dos ángulos, sino que puede servir como regla mnemotécnica para el momento de emplear estas identidades en otros cálculos. La demostración deberá realizarse por el método geométrico correspondiente, (el cual, lógicamente, no recuerdo con facilidad y en poco tiempo, generalmente corto en un examen). Cuando los nervios traicionan y el tiempo es escaso, puede venir bien este sistema, antes que apelar a alguna chuleta, la mejor chuleta es la que se queda en mente.

Es más sencillo recordar que el producto de dos números complejos, expresados en la forma (a +bi) * (c + di) da como resultado:

z¹ * z² = (a +bi) * (c+ di) = (a * c - b * d , a * d + b * c) donde se destaca una parte REAL y otra IMAGINARIA. (a * c - b * d) es la PARTE REAL y (a * d + b * c) es la parte IMAGINARIA.

Si expresamos los números complejos de módulo 1 de la forma z¹ = [cos x + i sen x] y el otro z²= [cos y + i sen y]. Tendremos que su producto, es decir la suma de sus ángulos, es el resultado de la operación (a * c menos b * d) para el cálculo de la parte real, o sea, el coseno; y (a * d + b * c) para el cálculo de la parte imaginaria, o sea, el seno. Por tanto:

Cálculo de la parte imaginiaria de la suma y resta de dos ángulos:
sen (x+y) = [cos x + i sen x] * [cos y + i sen y] = (a * d + b * c) , por tanto:
[1] sen (x+y) = [cos x * senx + sen y * cos y]
sen (x - y) = [cos x + i sen x] * [ cos -y + sen -y] = (a * d + b * c), por tanto, y teniendo en cuenta que cos -y = cos y, y que sen -y = -sen y.
[2] sen(x-y)=[cos x * (- sen y) + sen y * cos y] = [ sen y * cos y - cos x * sen y] 

Cálculo de la parte real de la suma y resta de dos ángulos:
cos (x+y) = [cos x + i sen x] * [cos y + i sen y] = (a * c - b * d) , por tanto:
[3] cos (x+y)= [ cos x * cos y - sen x * sen y]
cos (x - y) = [cos x + i sen x] * [cos -y + i sen -y] = (a * c - b * d) , por tanto:
[4] cos (x - y) = [ cos x * cos y + sen x * sen y].

Con lo cual tenemos un sistema rápido para recordar la equivalencia de estas funciones trigonométricas en un momento dado sin recurrir demasiado a la memoria. Con estas cuatro ecuaciones es fácil deducir las de la tangente y los ángulos doble. También permiten aplicar las siguientes tres ecuaciones muy necesarias para el cálculo de Integrales con integrandos formados por productos de funciones trigonométricas compuestas, del tipo:

INT ( sen 3x * cos x * sen 2x) * dx.

El cual veremos cómo hallar su función primitiva por medio de estas tres ecuaciones:

[5] sen x * cos y = 1/2 [ sen (x+y) - sen ( x - y)]
[6] sen x * sen y = 1/2 [ cos (x - y ) + cos (x + y)]
[7] cos x * cos y = 1/2 [ cos (x + y) + cos ( x - y)].

INT (sen 3x * cos x * sen 2x) * dx. Para resolver esta Integral indefinida nos limitaremos a utilizar las fórmulas [6] y [7] para transformar potencias en funciones trigonométricas de producto de ángulos que son integrables de forma inmediata.
1º PASO): La expresión sen 3x * sen 2x, aplicando [6] queda en:
sen 3x * sen 2x = 1/2 [ cos( 3x-2x) - cos (3x+2x)] y deja la integral de esta forma:
INT (1/2 [ cos( 3x-2x) - cos (3x+2x)]) * cos x * df y operando expresiones queda:
INT (1/2 (cos x - cos 5x ) * cos x * df

2º PASO): Si resolvemos los productos eliminamos factores y podremos expresar la integral como sumandos de integrales inmediatas, esa es la idea. Por tanto calculamos el producto:
(1/2 (cos x - cos 5x ) * cos x = 1/2 cos x * cos x - 1/2 cos 5x * cos x
y la integral queda así:
INT (1/2 cos² x - 1/2 cos 5x * cos x) *df y separando sumandos en dos integrales A y B, tal que A - B:
(A) INT (1/2 cos² x ) * df - (B) INT (1/2 cos 5x * cos x) *df

3º PASO): Resolvemos ahora los productos de A para reducir la potencia a una expresión que se pueda integrar directamente, y expresamos, aplicando [7]:

cos² x = 1/2 ( 1 + cos 2x) y queda la integral A:

INT (1/4 + 1/4 cos 2x) *df y separando en sumandos de la forma A¹ + A²:

(A¹) INT 1/4 * df + (A²) INT 1/4 cos 2x *df

Hacemos lo mismo con la Integral (B) aplicando [7] resolvemos que:

cos 5x * cos x = 1/2 (cos 4x + cos 6x) y queda la integral (B) así:

(B) INT [(1/4 cos 4x) + ( 1/4 cos 6x)] * df. Y aplicando la prop. de las suma de integrales, dejamos (B) en función de B¹ + B²:

(B¹) INT 1/4 cos 4x * df + (B²) INT 1/4 cos 6x * df

4º PASO) Expresamos ahora todo junto: A¹ - A² + B¹ + B² :

INT 1/4 * df + INT 1/4 cos 2x *df - INT 1/4 cos 4x * df + INT 1/4 cos 6x * df

Y ya se puede integrar directamente cada una dando como resultado:

INT ( sen 3x * sen 2x * cos x) *df = (x/4) + (sen 2x/8) - (sen 4x/16) - (sen 6x/16) + K , K constante.

No se si ha quedado muy claro pero esa es la idea.

Con integrales del tipo sen² x * cos³ x se procede de forma diferente aunque la idea es la misma, reducir potencias, resolver productos, expresar sumandos e integrar directamente. En el caso particular de que tan sólo uno de los factores de la integral sea potencia negativa se suele resolver mediante el método de cambio de variable del tipo:

t= sen x ó t = cos x, dependiendo si el factor de potencia impar es el sen o cos.

En caso de que los factores tengan ambos potencias pares, básicamente se resuelven partiendo de la transformación que define la siguiente escuación [8] que relaciona el producto de un sen² x * cos ² x de una forma útil de manejar:

[8] sen² x * cos ² x = 1/4 * (sen² 2x).

 

BLOQUES DE ALGEBRA Y GEOMETRIA

Vectores geométricos en el plano

Longitud y dirección, operaciones, aplicaciones a la geometría

En un sistema de ejes cartesianos, cada punto se describe mediante sus coordenadas.

Dados los puntos A y B, la flecha que va de A a B se llama vector, se representa por AB. A es el origen del vector y B el extremo.

Para calcular las coordenadas del vector AB, se restan las coordenadas del extremo menos las del origen.

Si el origen del vector es el origen de coordenadas (0,0), las coordenadas del extremo son las coordenadas del vector.

Un vector es un segmento orientado que va del punto A (origen) al punto B (extremo).

Todo vector se compone de un módulo, una dirección y un sentido.

Dirección de un vector

Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Sentido de un vector

El sentido del vector AB es que va del origen A al extremo B.

Módulo de un vector

El módulo del vector AB longitud del segmento AB .

El módulo de un vector es un número siempre positivo o cero.

 

 

Operaciones Básicas con Vectores

Se deben especificar tanto su magnitud (número) como su dirección, que se pueden especificar con solo el número. Cualquier conjunto de vectores del mismo tipo, (que tengan las mismas unidades) se puede combinar por medio de las operaciones básicas con vectores.

 

APLICACIONES DE LA GEOMETRIA

 

La Geometría estudia las formas de las figuras y los cuerpos geométricos.

 En la vida cotidiana encontramos modelos y ejemplificaciones físicas de esos objetos ideales de los que se ocupa la Geometría, siendo muchas y variadas las aplicaciones de esta parte de las matemáticas.

   

INDICADORES DE LOGRO: Interpreta los elementos que determina un vector. Aplica las nociones de magnitud y dirección en un segmento de recta en un plano. Interpreta gráficamente un enunciado vectorial dado en lenguaje natural. Traduce correctamente la información que suministra un gráfico convectores.

 

RED DE CONCEPTOS: Vectores en R2, elementos, ubicación en el plano cartesiano, operaciones en geometría y en álgebra con vectores.

 

CONCEPTOS PREVIOS: Geometría plana (ángulos y triángulos), Geometría analítica (Plano cartesiano y rectas), razones trigonométricas y solución triangular aplicando teoremas del seno y del coseno.6.

 

PROCEDIMENTALES

Reconocimiento de cantidades vectoriales

Diferenciación de cantidades escalares de cantidades vectoriales

Representación de cantidades vectoriales mediante el algebra

El cálculo de la magnitud o norma de un vector.

Reconocimiento de vectores equivalentes

Representación de desplazamientos y fuerzas en el plano coordenado bidimensional

.Determinación en un par ordenado que representa un vector, su norma, dirección y sentido.

Representación vectorial de un desplazamiento o de una fuerza

Trazar vectores gráficamente a escala adecuada

Determinación de la equipolencia de un vector mediante trabajo algebraico de pares ordenados

Como sumar cantidades vectoriales gráficamente y analíticamente

Como restar cantidades vectoriales gráficamente y analíticamente

Como multiplicar vectores por cantidades escalares

Como dividir cantidades vectoriales por cantidades escalares

Traduce cantidades vectoriales descritas verbalmente

Representación en el plano de cantidades vectoriales descritas

verbalmente.

 

El espacio R2: operaciones algebraicas, identificación con vectores geométricos.

Longitud de un vector y distancia entre dos puntos

                 

 

Bloque de Matemáticas Discretas

1.    PROGRAMACION LINEAL

La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.

Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.

 

CONJUNTO FACTIBLE

El conjunto intersección, de todos los semiplanos formados por las restricciones, determina un recinto, acotado o no, que recibe el nombre de región de validez o zona de soluciones factibles.

 

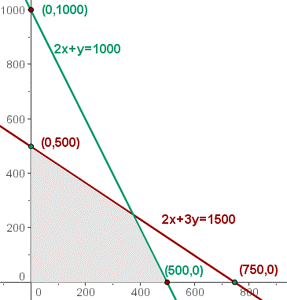
FUNCIÓN OBJETIVO

En esencia la programación lineal consiste en optimizar (maximizar o minimizar) una función objetivo, que es una función lineal de varias variables:

f(x,y) = ax + by.

RESTRICCIONES

La función objetivo está sujeta a una serie de restricciones, expresadas por inecuaciones lineales:

	a1x + b1y ≤ c1
	a2x + b2y ≤c2
	...    ...    ...
	anx + bny ≤cn

Cada desigualdad del sistema de restricciones determina un semiplano.

 

SOLUCIÓN ÓPTIMA

El conjunto de los vértices del recinto se denomina conjunto de soluciones factibles básicas y el vértice donde se presenta la solución óptima se llama solución máxima (o mínima según el caso).

 

VALOR DEL PROGRAMA LINEAL

El valor que toma la función objetivo en el vértice de solución óptima se llama valor del programa lineal.

 

Bloque De Estadística Y Probabilidad

6. PROBABILIDAD

FRECUENCIA

En estadística se pueden distinguir hasta cuatro tipos de frecuencias:

·         Frecuencia absoluta Es el promedio de una suma predeterminada y además consiste en saber cuál es el número o símbolo de mayor equivalencia. (n_i) de una variable estadística X_i, es el número de veces que este valor aparece en el estudio. A mayor tamaño de la muestra aumentará el tamaño de la frecuencia absoluta; es decir, la suma total de todas las frecuencias absolutas debe dar el total de la muestra estudiada (N).

·         Frecuencia relativa (f_i), es el cociente entre la frecuencia absoluta y el tamaño de la muestra (N). Es decir,

 

siendo el f_i para todo el conjunto i. Se presenta en una tabla o nube de puntos en una distribución de frecuencias.

Si multiplicamos la frecuencia relativa por 100 obtendremos el porcentaje o tanto por ciento (p_i)

·        Frecuencia absoluta acumulada (N_i), es el número de veces n_i en la muestra N.

·        Frecuencia relativa acumulada (F_i), es el cociente entre la frecuencia absoluta acumulada

 

Supongamos que las calificaciones de un alumno de secundaria fueran las siguientes:

18, 13, 12, 14, 11, 08, 12, 15, 05, 20, 18, 14, 15, 11, 10, 10, 11, 13. Entonces:

·         La frecuencia absoluta de 11 es 3, pues 11 aparece 3 veces.

·         La frecuencia relativa de 11 es 0.17, porque corresponde a la división 3/18.

 

REPRESENTACION GRAFICA

 

Una gráfica es la representación en unos ejes de coordenadas de los pares ordenados de una tabla.

Las gráficas describen relaciones entre dos variables.

La variable que se representa en el eje horizontal se llama variable independiente o variable x.

La que se representa en el eje vertical se llama variable dependiente o variable y.

La variable y está en función de la variable x.

Una vez realizada la gráfica podemos estudiarla, analizarla y extraer conclusiones.

Para interpretar una gráfica, hemos de observarla de izquierda a derecha, analizando cómo varía la variable dependiente, y, al aumentar la variable independiente, x.

Kg de patatas	1	2	3	4	5
Precio en €	2	4	6	8	10

 

En esa gráfica podemos observar que a medida que compramos más kilos de patatas el precio se va incrementando.

 

Nota	0	1	2	3	4	5	6	7	8	9	10
Nº de alumnos	1	1	2	3	6	11	12	7	4	2	1

 

En esta gráfica observamos que la mayor parte de los alumnos obtienen una nota comprendida entre 4 y 7.

PROBABILIDAD

La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.

SUCESO

Es cada uno de los resultados posibles de una experiencia aleatoria.

Al lanzar una moneda salga cara.

Al lanzar una moneda se obtenga 4.

SUCESO ALEATORIO

Suceso aleatorio es cualquier subconjunto del espacio muestral.

Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.

Ejemplo

Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:

1. El espacio muestral.

E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}

2. El suceso A = {extraer tres bolas del mismo color}.

A = {(b,b,b); (n, n,n)}

3. El suceso B = {extraer al menos una bola blanca}.

B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}

4. El suceso C = {extraer una sola bola negra}.

C = {(b,b,n); (b,n,b); (n,b,b)}

TECNICA DE CONTEO

El principio fundamental en el proceso de contar ofrece un método general para contar el numero de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

 

Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento Bpuede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a  n1 x n2.
 

¿De cuántas maneras pueden repartirse 3 premios a un conjunto de 10 personas, suponiendo que cada persona no puede obtener más de un premio?

Aplicando el principio fundamental del conteo, tenemos 10 personas que pueden recibir el primer

premio. Una vez que éste ha sido entregado, restan 9 personas para recibir el segundo, y

posteriormente quedarán 8 personas para el tercer premio. De ahí que el número de maneras

distintas de repartir los tres premios.

 

n

10 x 9 x 8 = 720

¿Cuántas placas de automóvil se pueden hacer utilizando dos letras seguidas de tres cifras? No se

admiten repeticiones.

 

26 x 25 x 10 x 9 x 8 = 468000

 

n un número entero positivo, el producto n (n-1) (n-2)...3 x 2 x 1 se llama factorial de n.

El símbolo ! se lee factorial y es el producto resultante de todos los enteros positivos de 1 a n; es decir, sea 

n

5! = 5 x 4 x 3 x 2 x 1 = 120

Por definición 0! = 1

 

 Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.

Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.

 

 Para facilitar el conteo examinaremos tres técnicas:

 

* La técnica de la multiplicación

* La tecnica aditiva
* La tecnica de la suma o Adicion

* La técnica de la permutación

* La técnica de la combinación. 

 

ESPACIO DE PROBANILIDAD

 

Sea  d el espacio muestral, que contiene n elementos {a₁, a₂, a₃,.....,a_n}, si a cada uno de los elementos de d le asignamos una probabilidad p_i ³ 0, entonces estamos transformando este espacio muestral en un espacio finito de probabilidad; el que debe cumplir con las siguientes características:

 

1)    Las probabilidades asociadas a cada uno de los elementos de d deben ser mayores o iguales a cero, p_i³0.

2)    La sumatoria de las probabilidades asociadas a cada uno de los elementos de d debe de ser igual a 1.

Sp_i = 1

 

 

Ejemplos:

1.Se lanza al aire un dado normal, si la probabilidad de que aparezca una de sus caras es proporcional al número que ostenta, a) ¿cuál es la probabilidad de que aparezca un número par?, b) ¿cuál es la probabilidad de que aparezca un número primo?

 

Solución:

 

                        d = {1, 2, 3, 4, 5, 6}

 

En este caso asignaremos las probabilidades como sigue;

 

p(aparezca el número 1) = p,  p(aparezca el número 2) = 2p, .....,

p(aparezca el número 5) = 5p, p(aparezca el número 6) = 6p

Y por ser d un espacio finito de probabilidad, entonces,

 

p(d) = p + 2p +  3p + 4p + 5p + 6p =1

 

Por tanto,   21p = 1, luego,  p = 1/21

 

a.       Luego;

 

A = evento de que aparezca un número par = {2, 4, 6}

 

p(A)=p(2)+p(4) + p(6) = 2p + 4p + 6p = 12p = 12(1/21) = 12/21= 0.5714

b.      B = es el evento de que aparezca un número primo = {1, 2, 3, 5}

p(B)=p(1) + p(2) + p(3) + p(5) = p + 2p + 3p + 5p = 11p = 11(1/21) = 11/21 = 0.5238

2. En una competencia de nado sincronizado, participan los equipos de Ecuador, México y Venezuela, México tiene el doble de posibilidades de ganar que Ecuador, mientras que Venezuela tiene un tercio menos de posibilidades de ganar que ecuador, a. Determine la probabilidad de que gane Venezuela, b. Determine la probabilidad de que gane Ecuador o Venezuela, c. Determine la probabilidad de que no gane México.

Solución:

                        d = {Ecuador, México Venezuela}

Por ser un espacio finito de probabilidad, p(d) = 1, luego,

P(d) = p(gane Ecuador) + p(gane México) + p(gane Venezuela) = p + 3p + 2/3p=1

Como 14/3p = 1,                 luego p = 3/14

a. p(gane Venezuela) = 2/3 p = 2/3*3/14 = 2/14 = 1/7 = 0.14285

b. p(gane Venezuela o Ecuador)=p(gane Venezuela)+p(gane Ecuador)=

 p(gane  Venezuela o Ecuador)= 2/3p + p = 5/3 p = 5/3*3/14 =5/14 = 0.35714

c. p(no gane México) = p(gane Venezuela o Ecuador) = 1 – p(gane México) = 1 – 3p =

= 1 – 3(3/14) = 1 – 9/14  = 5/14 = 0.35714

 3. En una competencia de ciclismo participan A, B y C, A tiene el doble de posibilidades de ganar que B y B el doble que C, a. Determine la probabilidad de que gane B, b. Determine la probabilidad de que gane A o B.

 

Solución:

 

d={ A, B, C}, y por ser un espacio finito de probabilidad,

 

p(d) = p(gane A) + p(gane B) + p(gane C) = 4p + 2p + p = 1

 

Como 7p = 1,    luego, p = 1/7

 

a.       p(gane B) = 2p = 2(1/7) = 2/7 = 0.28571

 

b.      p(gane A o B) = 4p + 2p = 6p = 6(1/7) = 6/7 = 0.85714

 

Definición de Estadística

La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.

Un estudio estadístico consta de las siguientes fases:

Recogida de datos.

Organización y representación de datos.

Análisis de datos.

Obtención de conclusiones.

Conceptos de Estadística

Población

Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.

Individuo

Un individuo o unidad estadística es cada uno de los elementos que componen la población.

Muestra

Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.

Muestreo

El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.

Valor

Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.

Dato

Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz.